문제 링크
https://www.acmicpc.net/problem/17252
◆문제 해결 및 설명◆
문제 : 3의 거듭제곱의 합으로만 이루어져 있다면 YES, 아닐 시 NO를 출력하여라.
알고리즘 분류 : 수학, 부르트포스 알고리즘, 사칙연산
첫째 줄에 2,147,483,647보다 작거나 같은 음이 아닌 정수 N이 입력된다.
기본 int로는 해결 할 수 없어 int64_t를 <memory> 헤더를 통해서 선언해 사용하였다.
※ 0은 삼삼한 수가 아니다.
풀고 검색해보니 생각보다 푸는 법이 많았다는 걸 알 수 있었다.
첫째. 3^N > 3^(N-1) + ... + 3^(0)
내가 푼 방법인데, 3진수를 cpp에서 지원하지 않기 때문에 이를 구현하지 않고 풀 방법이 있나 생각하다 쓰게 되었다. 아래 표는 3의 거듭제곱을 N=4까지 차례대로 나열하였다.
| 3^0 | 3^1 | 3^2 | 3^3 | 3^4 |
| 1 | 3 | 9 | 27 | 81 |
3^N > 3^(N-1) +... + 3^(0) 이 성립됨을 알 수 있다.
문제를 풀기위해 입력받은 수에 3의 거듭제곱들을 빼서 0이 되면 삼삼한 수라고 출력하겠다.
이를 위해 입력받은 수보다 작은 3의 거듭제곱 중에서 가장 큰값 3^N을 빼준다.
(더 작은 3의 거듭제곱들을 다 빼도 0이 되지 않기 때문에 삼삼한 수를 만들려면 반드시 빼야 한다.)
이후 가공된 입력받은 수보다 작은 3의 거듭제곱 중에서 가장 큰 값 3^N 을 빼주는 것을 반복한다.
가공된 입력받은 수에 N(지수)이 0이 될 때까지 반복했을 때, 가공된 입력받은 수가 0이면 삼삼한 수임을 확인할 수 있다.
둘째, 재귀를 통한 모든 수 확인
2,147,483,647보다 작은 3의 거듭제곱 중 가장 큰 값은 3^19 이므로 재귀적으로 모든 삼삼한 수를 찾아서 모든 합의 경우를 재귀를 통해 만들어 준다.
내가 푼 것은 아니니 그림으로 도식화만 하겠다.
하나의 함수에서 2번 재귀 호출을 하는데, 왼쪽은 해당되는 3의 거듭제곱(깊이)을 더해주고, 오른쪽은 더하지 않고 호출한다.
쉽게 말해 3^(depth)를 더하는 경우, 안 더하는 경우를 탐색한다. O(2^19)

셋째, %3 연산
삼진수를 구현하지 않고 빠르게 삼진수를 이용하여 푸는 코드이다.
입력받은 수를 %3을 했을 때 나머지가 2이라면 이는 삼삼한 수가 될 수 없다. (임의의 3의 거듭제곱이 2번 들어갔기 때문에)
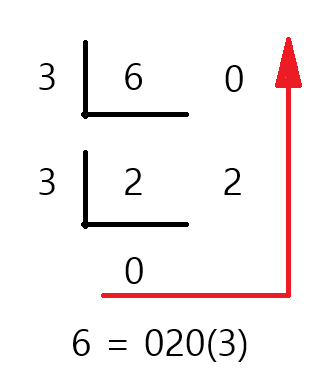
아래는 3진수를 구하는 방법을 사용한 6의 예시이다. 따라서 6은 삼삼한 수가 아니다.
◆코드 전문◆
#include <iostream>
#include <memory>
#include <cmath>
using namespace std;
int main()
{
int64_t N;
cin >> N;
// N == 0 case
if (N == 0)
{
cout << "NO";
return 0;
}
// 입력받은 수보다 작은 3의 거듭제곱 중에서 가장 큰값의 지수
int64_t numerical_index = -1;
for (int64_t i = 1; i <= N; i *= 3)
{
numerical_index++;
}
// 삼삼한 수인지 N에서 3의 거듭제곱을 빼서 확인
while (numerical_index + 1)
{
if (N >= pow(3, numerical_index))
N -= pow(3, numerical_index);
numerical_index--;
}
if (!N)
{
cout << "YES";
}
else
{
cout << "NO";
}
return 0;
}'코딩 공부 > 백준(C++)' 카테고리의 다른 글
| [백준 1245][C++] 농장 관리 (0) | 2023.10.21 |
|---|---|
| [백준 1987][C++] 알파벳 (1) | 2023.09.14 |
| [백준 1461][C++] 도서관 (0) | 2023.08.23 |
| [백준 10942][C++] 팰린드롬? (0) | 2023.08.11 |
| [백준 1911][C++] 흙길 보수하기 (0) | 2023.08.11 |
